Inhalt
Zur Verabschaulichung ausgwählter Themen aus dem Buchkapitel 4 in Farrell & Lewandowsky (2018) verwenden wir wieder unser Beispiel aus der Psychophysik (siehe letzte Stunde). In einem psychophysikalischen Experiment mit 30 Probanden beobachten wir folgende Werte zwischen physikalischem Reiz und Empfindung der Probanden.
In der Graphik wird zusätzlich zu den beobachteten Daten das Weber-Fechner Gesetz und ein lineares Regressionsmodell abgebildet. Sie können für beide Modelle in der Legende die Modellgleichung mit den besten Parameterwerten sehen.
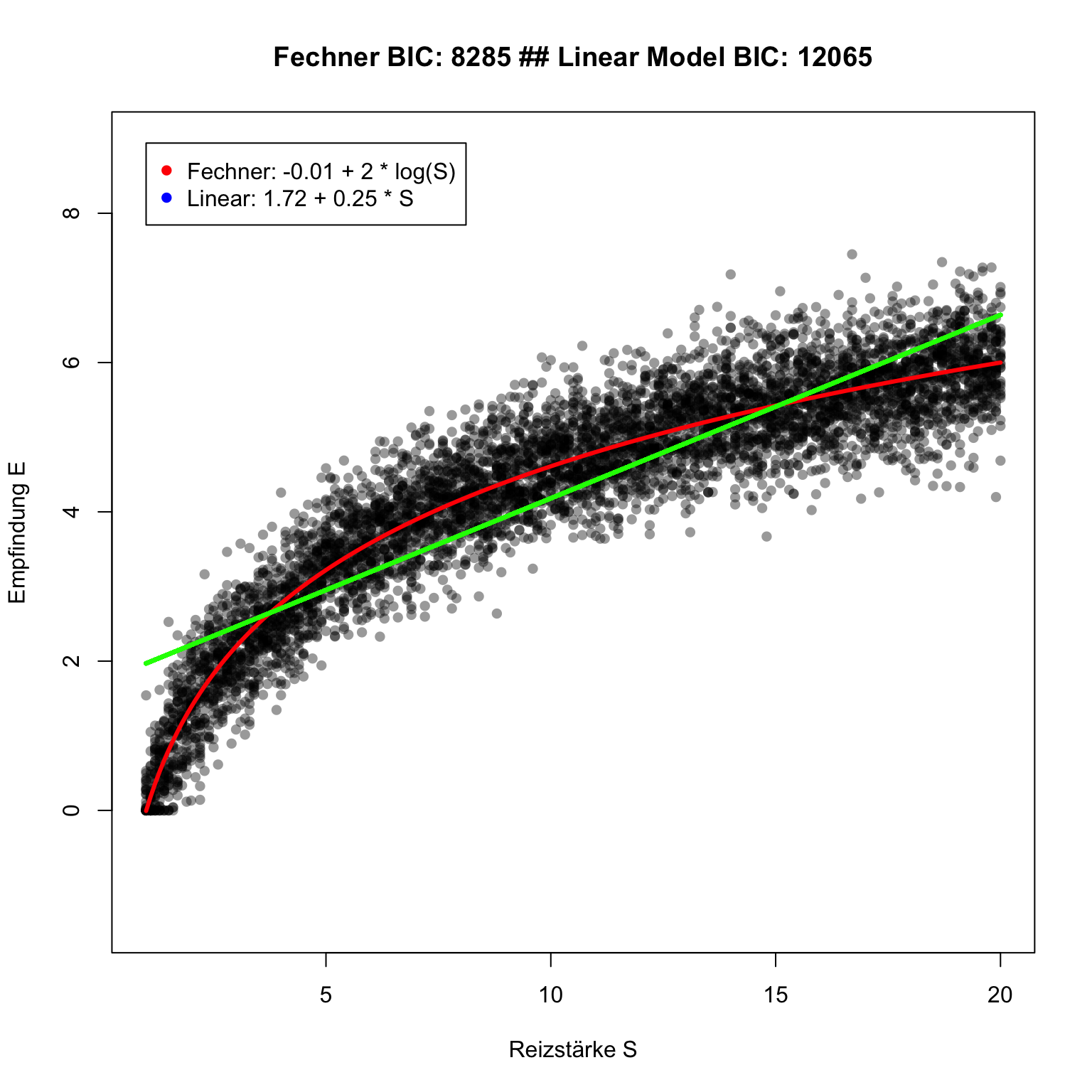
Wir schauen uns heute an, wie wir die besten Parameter für das Weber-Fechner Modell (\(a\) und \(b\) bei Weber-Fechner) aus den Daten mit Maximum Likelihood-Verfahren schätzen können.
Likelihood ist im Gegensatz zur mittleren Summe der quadrierten Abweichung in der Wahrscheinlichkeitstheorie verankert. Wenn man versteht, wie man basoeremd auf der Likelihood Modellparameter bestimmt, ist es nur noch ein kleiner Schritt zu einer Bayesianischen Analyse. In Farrell & Lewandowsky (2018) sind noch weitere Vorteile eines Maximum-Likelihood Schätzers für Modellparameter aufgelistet.
Abweichung Modell vs. Beobachtung
Wir nehmen einmal an, wir würden die besten Schätzungen für \(a\) und \(b\) im Weber-Fechner-Gesetz für unsere Daten kennen. Dann könnten wir ähnlich wie in der letzten Stunde die Differenz zwischen Vorhersage für die Empfindung \(E\) und die Modellvorhersae für \(E\) berechnen.
In der folgendne animeirten Graphik sieht man auf der linken Seite die Daten und das Weber-Fechner Gesetz. Die Differenz zwischen beobachteten Empfindungsstärken und Modellvorhersagen (= Residuen) werden auf der rechten Seite der Graphik abgetragen.
Wenn wir annehmen, dass die Differenzwerte normalverteilt sind, können wir Aussagen darüber machen, wie wahrscheinlich die Daten für bestimmte Parametertwerte im Weber-Fechner-Gesetz sind. Um das zu verstehen, schauen wir uns die Dichtefunktion der Normalverteilung an.
Dichtefunktion für normalverteilte Daten
Die Dichtefunktion der Normalverteilung ist durch folgende Gleichung definiert.
\[p(d|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \times e^{-(\text{d} -\mu)^2/(2\sigma^2)}\]
Zum Beispiel sieht die Dichtefunktion für \(\mu = 0\) und \(\sigma = 2\) folgendermaßen aus.
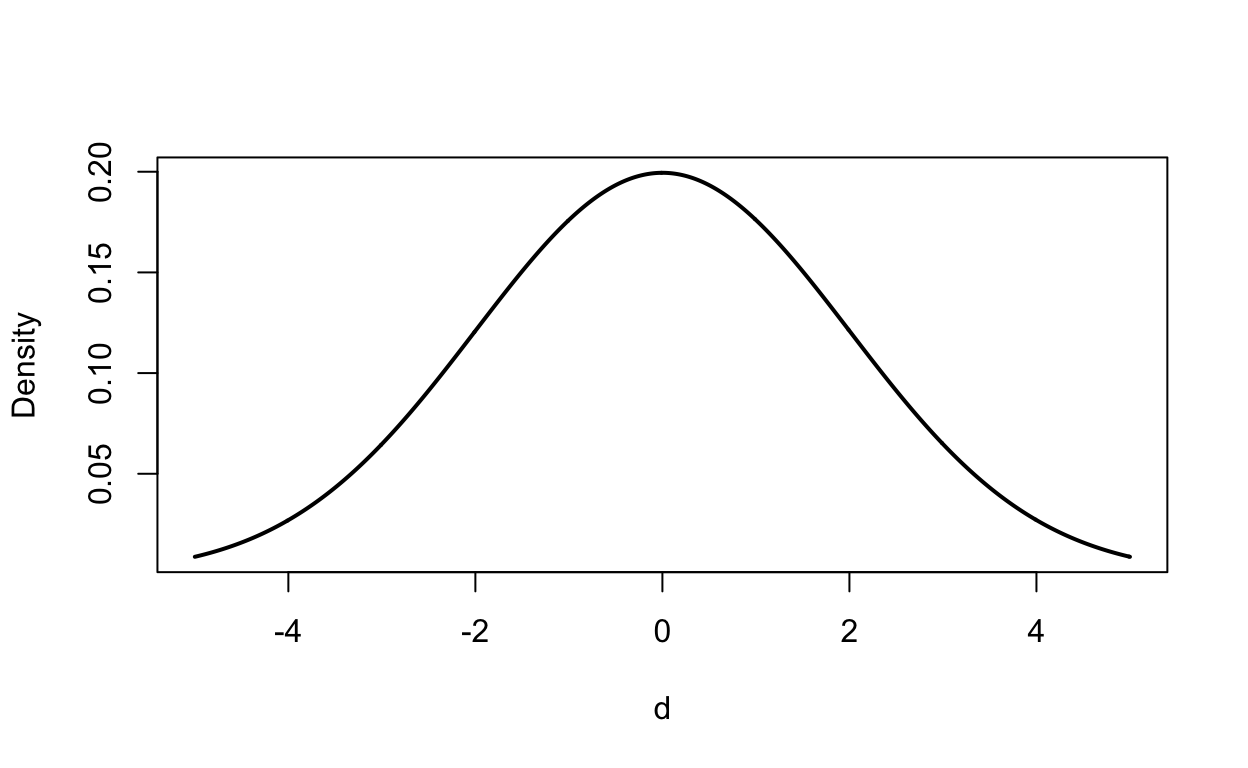
In der Dichtefunktion können wir also die Dichte für einen Datenpunkt bestimmen. Die Form der Funktion ist durch die beiden Parameter \(\mu\) und \(\sigma\) der Funktion definiert
Likelihood für normalverteilte Daten
Die Likelihoodfunktion ist identisch zur Dichtefunktion. Der inhaltliche Unterschied zwischen beiden Funktionen ist subtil: Die Likelihood-Funktion beschreibt, wie sich die Dichte für einen Punkt für verschiedene Ausprägungen der Parameterwerte \(\mu\) und \(\sigma\) verändert.
\[L(\mu,\sigma^2|d) = \frac{1}{\sqrt{2\pi\sigma^2}} \times e^{-(\text{d} -\mu)^2/(2\sigma^2)}\]
Die Likelihood für verschiedene Werte von \(\mu\) bei einem \(\sigma = 2\) bei einem beobachteten Datenpunkt von \(d = 3\) lässt sich aus der Likelihood-Funktion ablesen.
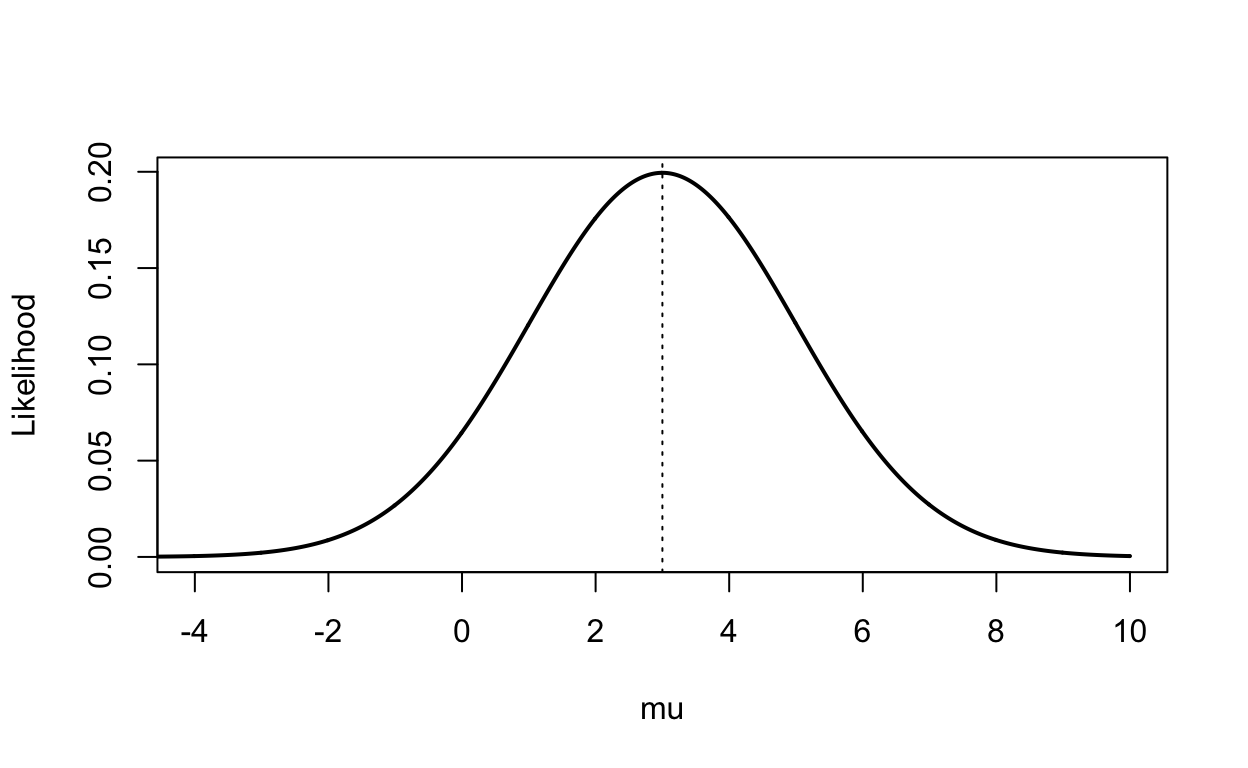
Die Likelihood-Funktion für verschiedene Werte von \(\sigma\) bei einem \(\mu = 0\) und einem beobachteten Datenpunkt von \(d = 3\) sieht folgendermaßen aus.
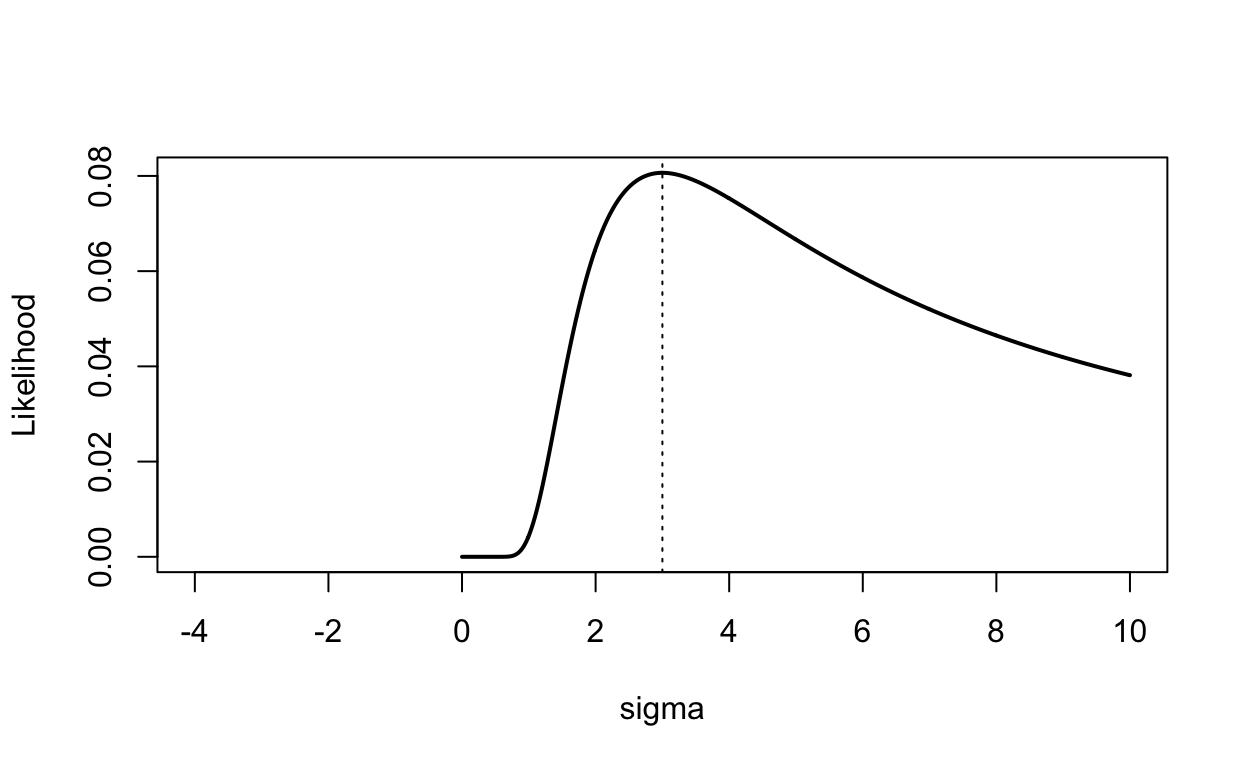
(Log-)Likelihood für mehrere Datenpunkte
Wenn wir nicht nur einen Datenpunkt vorliegen haben (im Experiment haben wir ja immer mindestens eine Beobachtung pro Proband), müssen wir die Gesamt-Likelihood für alle Daten berechnen.
Diese ist recht einfach zu bestimmen, indem man alle Likelihood-Werte miteinander multipliziert.
\[L(\theta|D) = L(\theta|d_1) \times L(\theta|d_2) \times \ldots \times L(\theta|d_n) \]
Da die Multiplikation von kleinen Zahlen zu immer kleineren Zahlen führt, die sich der 0 annähern, rechnet man nicht die Multiplikation aller Likelihood-Werte sondern die Summe aller log-Likelihood Werte. Das Maximum der Likelihood-Funktion und der Log-Likelihood-Funktion in Abhängigkeit der Parameterwerte ist identisch, daher dürfen wir diesen leinen Trick anwenden.
\[log[L(\theta|D)] = log[L(\theta|d_1) \times L(\theta|d_2) \times \ldots \times L(\theta|d_n)] =\] \[= log[L(\theta|d_1)] + log[L(\theta|d_2)] + \ldots + log[L(\theta|d_n)] \]
Die Summe der log-Likelihood Werte fasst also zusammen, wie wahrscheinlich die Daten für gegebene Parameterwerte sind.
Abweichungen aus dem psychophysikalischen Experiment
Kommen wir nun zurück zu unserem psychophysikalischen Experiment: Wir übertragen die Residuen, um die log-Likelihood der Daten zu bestimmen.
Wir nehmen an, die Residuen seien normalverteilt. Nun müssen wir im nächsten Schritt die Parameterwerte finden, die die Log-Likelihood Funktion in Bezug auf den Mittelwert und die Streuung der Daten maximiert. Dieses Vorgehen ist in der folgenden Graphik veranschaulicht.
Wenn wir zwei freie Parameter fitten (hier im Beispiel Mittelwert und Streuung), liegt eine Likelhood Fläche vor. Diese ist für unsere Daten in der folgenden Graphik geplottet.
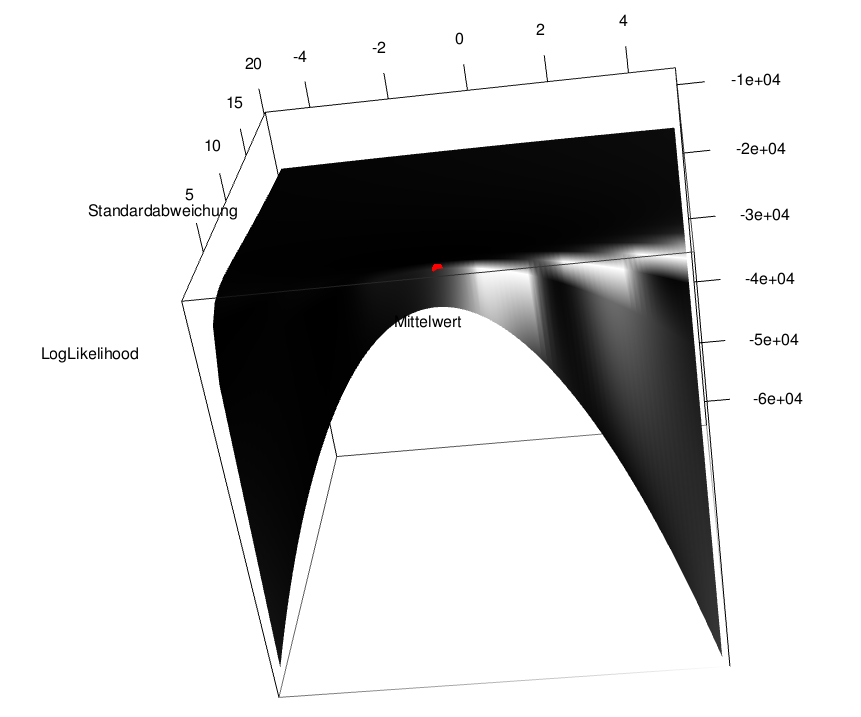
Für einen interaktiven Plot können Sie die folgende Funktion herunterladen und in R ausführen
Die Kombination der Parameterwerte, der zum höchten Punkt auf der Fläche führt (im Beispiel ist das ungefähr bei Mittelwert = 0 und Streuung = 2), ist der Maximum Log-Likelihood Wert (hier mit einen roten Punkt markiert).
Optimierung in R
Über diese Fläche können wir wieder unsere klugen Algorithmen laufen lassen (siehe letzte Stunde), der das Maximum der Fläche finden.
Per Konvention sucht die Optimierungsfunktion das Minimum der Fläche. Somit übergeben wir der Optimierungsfunktion nicht die Log-Likelihood Funktion sondern die negative Log-Likelihood Funktion.
Die negative log-Likelihood Funktion wird unten definiert.
Nun übergeben wir die negative Log-Likelihood Funktion der Optimierungsfunktion mle. Diese findet für uns die besten Parameterwerte.
Die Methode BFGS und die Kontrollargumente führen in der Regel zu guten Ergebnissen, diese können einfach übernommen werden. Die genauen mathematischen Details der Methode BFGS schauen wir uns nicht an.
Nachdem die Optimierungsfunktion das Minimum der Minus-Log-Likelihood Funktionen gefunden hat, können wir uns die Ergebnisse mit summary() anzeigen lassen.
summary(fit_ergebnis)
Maximum likelihood estimation
Call:
mle(minuslogl = opimierungs_funktion, method = "BFGS", control = list(maxit = 10^9,
reltol = 10^-9))
Coefficients:
Estimate Std. Error
standardabw 2.034929 0.0188129
-2 log L: 24913.97 Mit dem Befehl confint()lassen sich für die geschätzten Parameterwerte Konfidenzintervalle berechnen.
Optimierung Parameterwerte Weber-Fechner Gesetz in R
Wie kommen wir jetzt eigentlich genau auf die Parameterwerte des Weber-Fechner Gesetzes?
Die Likelihood-Funktion für Empfindung \(E\) eines physikalischen Reizes in Abhängigkeit der Modellparameter \(a\) und \(b\) ergibt sich aus folgender Gleichung.
\[L(\mu,\sigma^2|E) = \frac{1}{\sqrt{2\pi\sigma^2}} \times e^{-[\text{E} -\text{Vorhersage Fechner(a,b)}]^2/2\sigma^2}\]
Der Mittelwert \(\mu\) wird also einfach durch die Modellvorhersage des Weber-Fechner-Gesetzes ersetzt. Nun schauen wir uns wieder nicht nur einen Datenpunkt an, wir summieren die negativen log-Likelihood Werte für alle Empfindungen auf, um einen gesamten negativen Log-Likelihood Wert zu erhalten.Wir suchen dann wieder in mit Hilfe von R die Parameterwerte für \(a\), \(b\) und \(\sigma\), die die negative log-Likelihood Funktion minimieren.
minus_logLikelihood_Fechner = function(a=1, b=1, standardabw=1){
E_fechner = a + b * log(S)
minus_sum_loglik= -sum(dnorm(E_beobachtet,
mean = E_fechner ,
sd = standardabw,
log = TRUE))
return(minus_sum_loglik)
}
fitFechner = mle(minus_logLikelihood_Fechner,
method = "BFGS",
control = list(reltol = 10^-15, maxit = 10^9))
Hier kommt das Ergebnis unseres Fittings.
summary(fitFechner)
Maximum likelihood estimation
Call:
mle(minuslogl = minus_logLikelihood_Fechner, method = "BFGS",
control = list(reltol = 10^-15, maxit = 10^9))
Coefficients:
Estimate Std. Error
a -0.02452658 0.020873725
b 2.01241498 0.009210106
standardabw 0.49999961 0.004670588
-2 log L: 8317.525 Hier kommen die Konfidenzintervalle für alle Parameterwerte.
confint(fitFechner)
Profiling... 2.5 % 97.5 %
a -0.06544495 0.01639203
b 1.99436041 2.03046931
standardabw 0.49098161 0.50929406