Inhalt
In Kapitel 1 von Thagard (2000) wird die zentrale Hypothese darüber, wie Menschen denken, aus Sicht der Psychologie und Philosophie beschrieben. Folgendes Zitat auf S. 9-10 fasst dies gut zusammen:
The central hypothesis of cognitive science is that thought can be understood in terms of computational procedures on mental representations.
Um zu beschreiben und vorherzusagen, wie Menschen denken und handeln, brauchen wir demnach Modelle darüber, wie Menschen Dinge mental repräsentieren und welche Prozeduren sie nutzen, um die Repräsentation zu manipulieren.
Im Buch auf S. 10 steht dazu:
Although there is considerable dispute within cognitive science concerning what kinds of procedures and representations are most important for understanding mental phenomena, the computational/representational approach is common to current work on how mind can be understood in terms of rules, concepts, analogies, images, and neural networks (see Thagard 1996 for a concise survey).
Ein kognitiver Prozess—die Kohärenzmaximierung bei der Integration von Informationen—wird auf S. 3 anhand eines Beispiels—dem Kauf eines Autos—illustriert und von dem Inferenzschluss aus der Logik abgegrenzt.
Nach den Prinzipien der klassischen Logik sollten wir folgendermaßen vorgehen:
On the traditional account of inference that has been with us since Aristotle, your inferences are a series of steps, each with a conclusion following from a set of premises. Part of your chain of inference might be something like this: The seller looks honest. So the seller is honest. So what the seller says is true. So the car is reliable. So I will buy it.
Ein psychologisch plausbilerer Schluss sieht folgendermaßen aus:
Another view of inference understands it differently, not as the sort of serial, conscious process just described, but as a largely unconscious process in which many pieces of information are combined in parallel into a coherent whole. On this view, your inference about the car and its seller is the result of mentally balancing many complementary and conflicting pieces of information until they all fit together in a satisfying way. The result is a holistic judgment about the nature of the car, the nature of the seller, and whether to buy the car. Such judgments are the result of integrating the diverse information you have to deal with into a coherent total package. Whether you believe what the seller says about the car will depend in part on what you can infer about the car and vice versa.
Definition Kohärenz
In Kapitel 2 auf S. 17 in Thagard (2000) wird Kohärenz definiert.
Coherence can be understood in terms of maximal satisfaction of multiple constraints in a manner informally summarized as follows:
The elements are representations, such as concepts, propositions, parts of images, goals, actions, and so on.
The elements can cohere (fit together) or incohere (resist fitting together). Coherence relations include explanation, deduction, facilitation, association, and so on. Incoherence relations include inconsistency, incompatibility, and negative association.
If two elements cohere, there is a positive constraint between them. If two elements incohere, there is a negative constraint between them.
The elements are to be divided into ones that are accepted and ones that are rejected.
A positive constraint between two elements can be satisfied either by accepting both elements or by rejecting both elements.
A negative constraint between two elements can be satisfied only by accepting one element and rejecting the other.
The coherence problem consists of dividing a set of elements into accepted and rejected sets in a way that satisfies the most constraints.
In Thagard (2000) finden wir eine Tabelle, in denen Bereiche aufgelistet werden, in denen Kohärenzprozesse eine Rolle spielen.
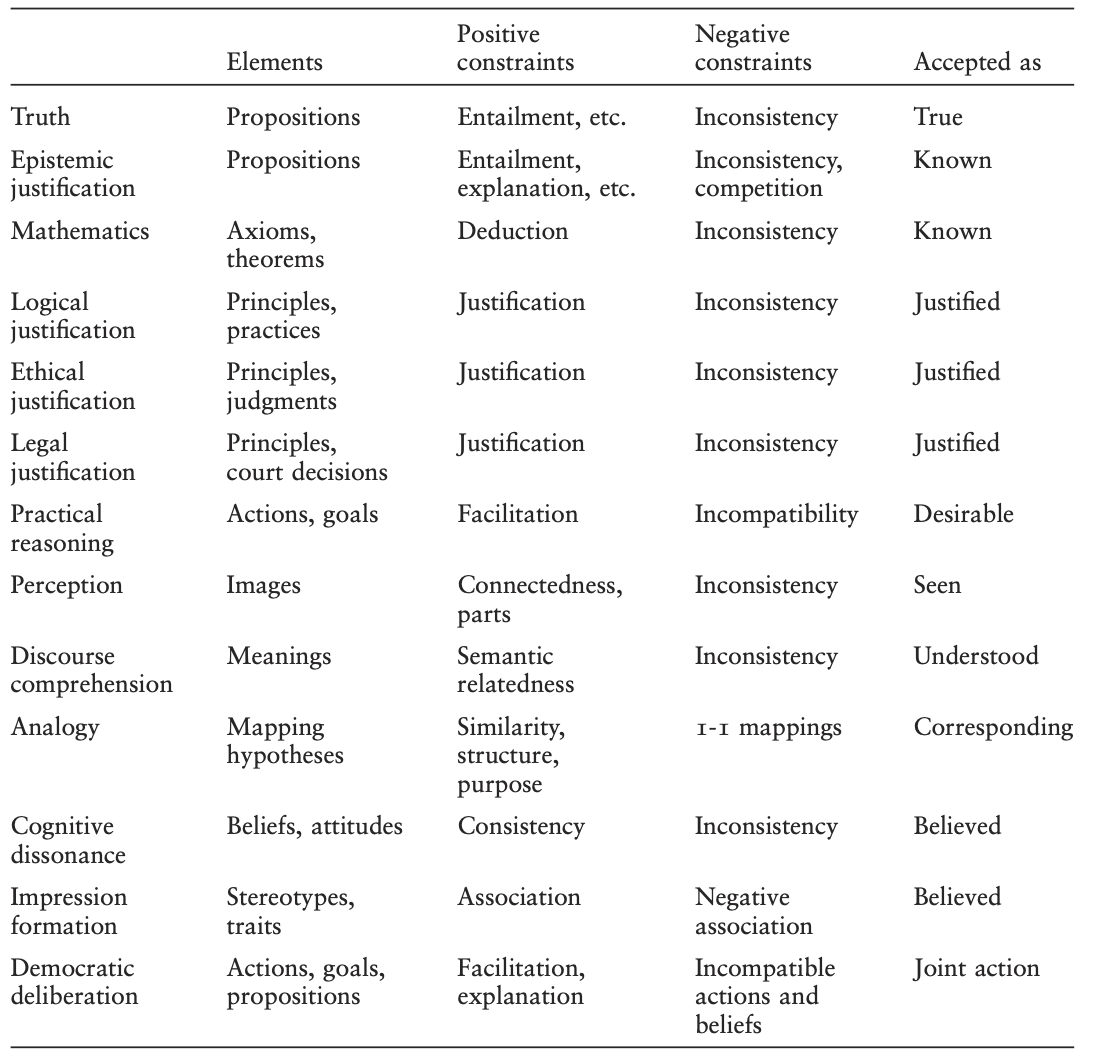
Kohärenzprozesse spielen also in basalen Bereichen wie z. B. der Wahrnehmung, wie auch in komplexeren Bereichen wie z. B. der Bewertung des Wahrheitsgehalts von Evidenz eine Rolle. Wir haben es also mit einem universellen kognitiven Mechanismus zu tun.
Operationalisierung von Kohärenz und Kohärenzmaximierung
In Kapitel 2 beschreibt Thagard (2000) fünf Algorithmen, wie sich die Kohärenz bei der Integration von Informationen maximieren lässt. Den konnektionistischen Algorithmus werden wir noch kennenlernen, wir lassen diesen hier aus. Beispielhaft schauen wir uns gemeinsam den ersten Ansatz—den exhaustiven Ansatz—an, um eine Idee davon zu bekommen, wie Kohärenz konkret operationalisiert werden kann.
Um den exhaustiven Ansatz zu verstehen, müssen wir die Berechnung der Kohärenz verstehen. Thagard (2000) schreibt dazu auf S. 18:
More formally, we can define a coherence problem as follows. Let E be a finite set of elements \(\{e_i\}\) and \(C\) be a set of constraints on \(E\) understood as a set \(\{(ei, ej)\}\) of pairs of elements of \(E\). \(C\) divides into \(C+\), the positive constraints on \(E\), and \(C-\), the negative constraints on \(E\). With each constraint is associated a number \(w\), which is the weight (strength) of the constraint.
The problem is to partition \(E\) into two sets, \(A\) and \(R\), in a way that maximizes compliance with the following two coherence conditions:
- If \((e_i, e_j)\) is in \(C+\), then \(e_i\) is in \(A\) if and only if \(e_j\) is in \(A\).
- If \((ei, ej)\) is in \(C-\), then \(e_i\) is in \(A\) if and only if \(e_j\) is in \(R\).
Let \(W\) be the weight of the partition, that is, the sum of the weights of the satisfied constraints. The coherence problem is then to partition \(E\) into \(A\) and \(R\) in a way that maximizes \(W\). Because a coheres with \(b\) is a symmetric relation, the order of the elements in the constraints does not matter.
Das sieht kompliziert aus, aber eigentlich ist es nicht so schwer zu verstehen. Schauen wir uns einmal ein Beispiel aus der Personenwahrnehmung an. Wie nehmen Sie zum Beispiel Bill Clinton wahr? Ein Element \(e_1\) Ihrer Wahrnehmung könnte zum Beispiel sein, dass Clinton ein intelligenter Mensch ist. Ein weiteres Element \(e_2\) Ihrer Wahrnehmung könnte sein, dass Clinton ein moralischer Mensch ist. Ein weiteres Element \(e_3\) könnte sein, dass Clinton ein unehrlicher Mensch ist.
Nehmen wir einmal an, dass die Verknüpfung zwischen \(e_1\) und \(e_2\) positiv ist, es handelt sich also um einen positiven Constraint \(C+\). Ein intelligenter Mensch ist eher moralisch. Die Stärke der Assoziation könnte man mit einem Gewicht \(w_{e_1,e_2}\) quantifizieren. Die Verknüpfung zwischen diesen beiden Elementen ist kohärent, wenn Sie denken, dass Clinton intelligent (= \(A\) für accept) und moralisch (\(A\)) ist. Die Verknüpfung wäre auch kohärent, wenn Sie denken, dass Clinton dumm (\(R\) für Reject) und unmoralisch (\(R\)) ist.
Schauen wir uns nun Element \(e_3\) an. Wenn Sie denken, dass moralische (\(A\)) und intelligente (\(A\)) Menschen ehrlich sind, also eine positive Verknüpfung zwischen \(e_3\) und \(e_1\) bzw. \(e_2\) mit einer Gewicht \(w_{e_1,e_3}\) bzw \(w_{e_2,e_3}\) vorliegt, dann passt Ihre Wahrnehmung \(e_3\) (\(R\)) nicht zu den anderen beiden Wahrnehmungen. Diese ist also inkohärent.
Wenn wir nun bestimmen möchten, wie kohärent Ihre Wahrnehmung für diese Situation insgesamt ist, können wir uns die Summe der Gewichte der kohärenten und der inkohärenten Relationen anschauen. Nehmen wir für unser Beispiel an, dass \(w_{e_1,e_2} = .5\) und \(w_{e_1,e_3} = .5\) und \(w_{e_2,e_3} = 1\) ist (d.h., moralisch und ehrlich ist stärker assoziiert als intelligent und moralisch und intelligent und ehrlich) sind.
Die Relation zwischen \(e_1\) und \(e_2\) ist die einzig kohärente Relation. Die Summe der Gewichte “aller” kohärenten Relationen beträgt daher \(w_{e_1,e_2}=.5\). Die Relation zwischen \(e_1\) und \(e_3\) sowie zwischen \(e_2\) und \(e_3\) sind inkohärent. Die Summe der Gewichte aller inkohärenten Relationen beträgt demnach \(w_{e_1,e_3} + w_{e_2,e_3} = .5 + 1 = 1.5\). Die Gesamtwahnrehmung ist also eher inkohärent (.5 vs. 1.5).
Menschen streben nach kohärenten Repräsentationen von Informationen.
Wie ließe sich die Kohärenz in Ihrer Wahrnehmung von Bill Clinton erhöhen?
Der exhaustive Algorithmus zur Bestimmung der kohärentesten Repräsentation ist recht simpel. Ich generiere alle möglichen Zustände von \(e_1\), \(e_2\) und \(e_3\) bei den gegebenen positiven und negativen Constraints durch (also z.B. \(\{A,A,A\}\), \(\{A,A,R\}\),\(\{A,R,A\}\),\(\ldots\),\(\{R,R,R\}\)) und kann für jede Kombination die Gesamtkohärenz berechnen. Die Repräsentation mit der höchsten Kohärenz ist die wahrscheinlichste Repräsentation, wenn Prinzipien der Kohärenzmaximierung bei der Personenwahrnehmung eine Rolle spielen.
Methoden
Im Folgenden werden wir ein Phänomen aus der Physik und ein Phänomen aus der Psychologie mit der Hilfe von formalisierten Modellen beschreiben. Dabei erhalten wir einen ersten Eindruck darüber, wie ein formalisiertes Modell aussieht und wie man damit umgehen kann, um interessante empirische Beobachtungen zu ordnen und Beobachtungen in der Zukunft vorherzusagen.
Phänomen: Bewegung von Planeten
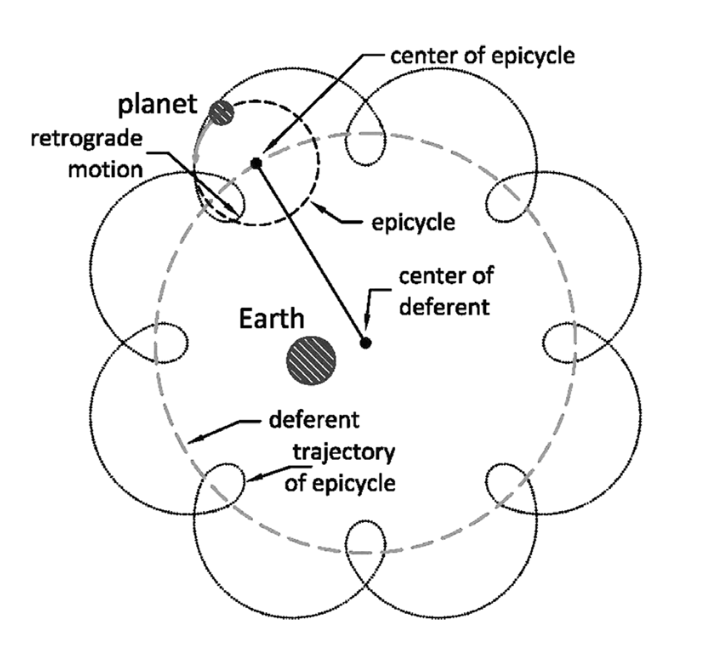
Wenn wir an den Himmel schauen, können wir beobachten, dass sich die Planeten unseres Sonnensystems von rechts nach links auf unserem Nachthimmel bewegen, dann für kurze Zeit in umgekehrter Richtung von links nach rechts und dann wieder von rechts nach links. Dieses Phänomen nennt man “retrograde Bewegung” und ist in der folgenden Abbildung angedeutet.

Modelle
Wie können wir nun das Phänomen der “retrograden Bewegung” mit einem Modell beschreiben?
Wir schauen uns dazu zwei Modelle an: Ein geozentrisches Modell, das annimmt, dass die Erde der Mittelpunkt unseres Planetensystems ist, und ein heliozentrisches Modell, das annimmt, dass die Sonne der Mittelpunkt unseres Planetensystems ist.
Modell 1: Geozentrisches Planetenmodell
Im geozentrischen Modell muss für die Erklärung der retrograden Bewegung angenommen werden, dass sich Planten, die um die Erde kreisen, in Schleifen bewegen. Dies ist in der unteren Abbildung angedeutet.
Modell 2: Heliozentrisches Planetenmodell
Im heliozentrischen Modell bewegen sich alle Planeten unseres Sonnensystems auf einem Kreis (später durch Kepler modifiziert: auf Ellipsen) mit unterschiedlicher Geschwindigkeit. Die scheinbare Rückwärtsbewegung ist eine Wahrnehmungsillusion, wie in der Abbildung unten angedeutet wird.
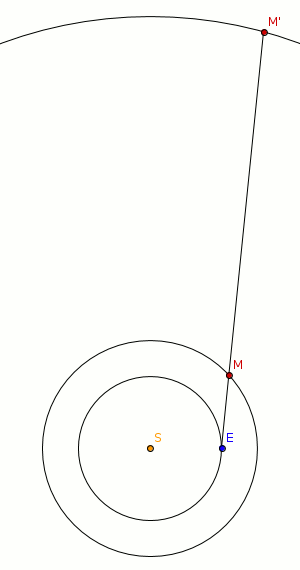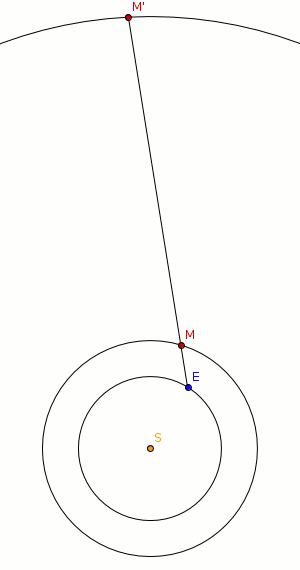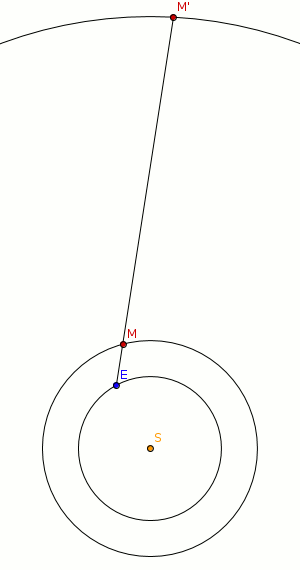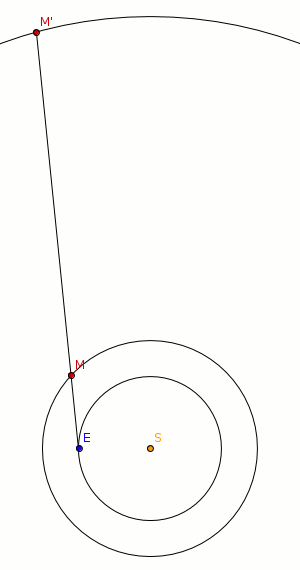
Die Erde (E) überholt den Mars (M). Wenn das passiert, läuft die Projektion des Mars (M’) auf den zu unserem Sonnensystem annähernd stabilen Sternenhintergrund für kurze Zeit in die der Erde entgegengesetzten Richtung. Das Phänomen lässt sich also ohne die Annahme, dass Planeten ihre Bewegungsrichtung ändern (warum sollten sie dies auch tun?), erklären.
Bewertung Modelle
Welches ist nun das bessere Modell? Beide Modelle können annähernd gut die Position von Planeten beschreiben und vorhersagen. Die Vorhersagegüte (“goodness of fit”) ist nahezu identisch. Dieses wichtige Kriterium bei der Selektion eines Modells können wir also nicht heranziehen.
Zwar wissen wir heutzutage, dass das heliozentrische Modell korrekt ist, aber versetzen Sie sich in eine Forscherin, die vor den ersten Aufnahmen aus dem Weltraum gelebt hat. Die Modelle sind nicht direkt überprüfbar, da die Bestandteile (= Planeten) und ihre Relationen (= Positionen und Bewegungen) nicht direkt beobachtbar sind. Die Modelle sind also nur in unserem Kopf.
Gibt es noch weitere Kriterien, die wir anwenden können, um zu entscheiden, welches Modell besser ist?
Phänomen: Kategorisierung
In einer Studie von Nosofsky (1991) wurden den Probanden in einer Lernphase Gesichter gezeigt, die sich auf mehreren Ausprägungen bei Features (z. B. Distanz der Augen voneinander, Länge der Nase, etc.) unterscheiden wie in der folgenden Abbildung dargestellt.
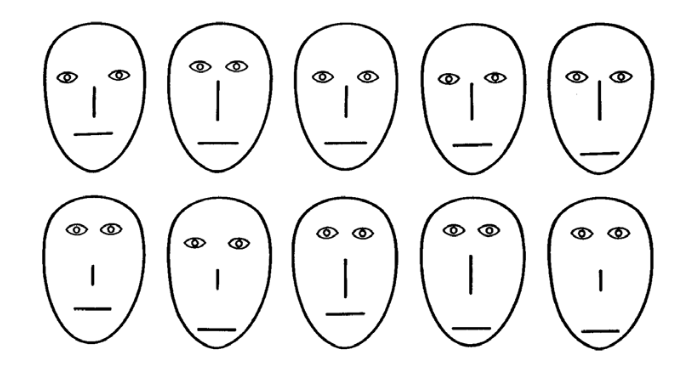
Jedes Gesicht gehört zu einer “Familie,” zu welcher Familie das Gesicht gehört, wurde den Probanden in der Lernphase zurückgemeldet. In der Testphase wurden nun neue und alte Gesichter gezeigt. Die Probanden sollten angeben, ob sie das Gesicht schon einmal gesehen haben (= Rekognition) und zu welcher Familie das Gesicht gehört (= Kategorisierung).
Der Zusammenhang zwischen der mittleren Klassifikationswahrscheinlichkeit (unabhängig davon, ob das Gesicht zu Familie 1 oder 2 zugeordnet wurde) und der Antwort “habe ich schon in der Lernphase gesehen” ist in der folgenden Graphik abgetragen. Warum plottet man das? Die Idee ist, dass Gesichter, die eindeutig einer Familie zugeordnet werden, auch eher als “schon gesehen” eingeordnet werden oder umgekehrt, dass als “schon gesehen” eingeschätzte Gesichter eindeutiger einer Familie zugeordnet werden können.
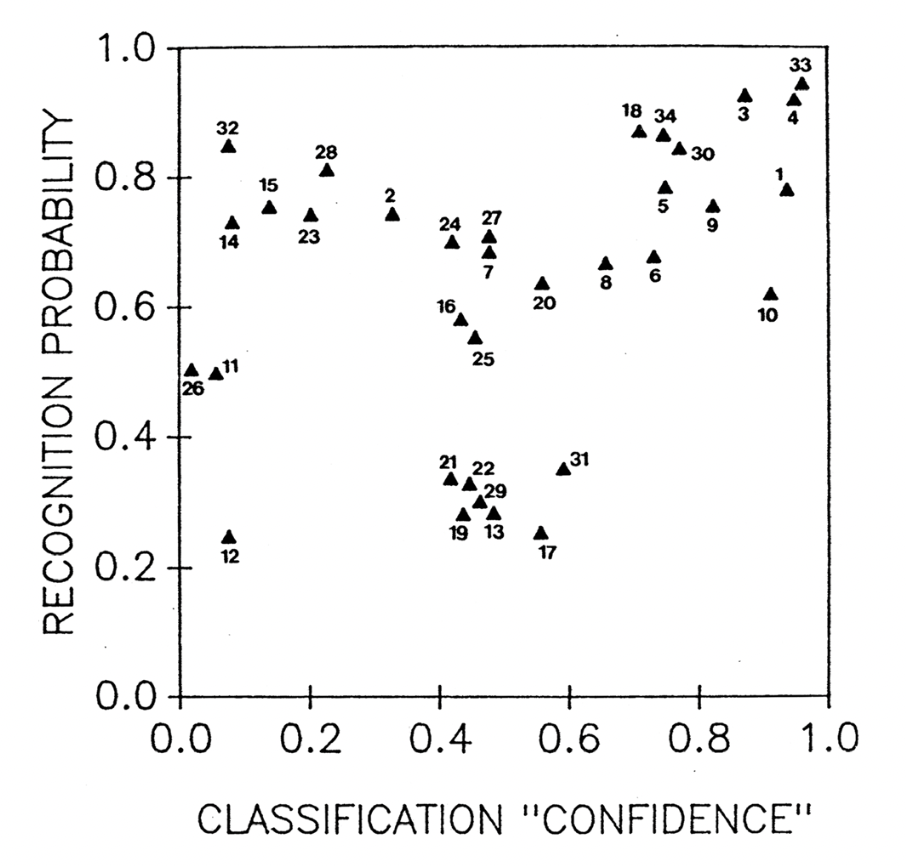
Man kann eine leichte positive Korrelation beobachten: Je höher die Klassifikationswahrscheinlichkeit, desto höher die Wahrscheinlichkeit das Gesicht als “schon gesehen” einzuschätzen.
Modell
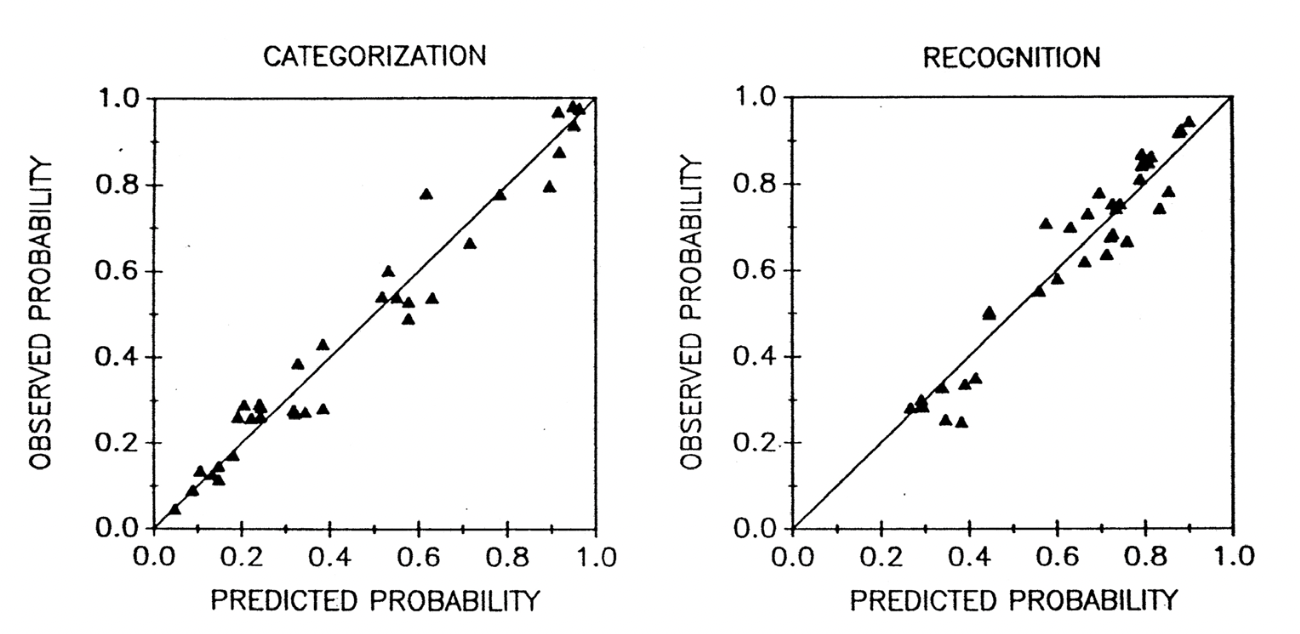
Wenn man das Exemplarmodell von Nosofsky (1991) auf die Daten anwendet, sieht man in der folgenden Abbildung, dass das Modell (hier auf der x-Achse) die beiden Messvariablen (hier auf der y-Achse) nahezu perfekt vorhersagen kann. Kategorisierung und Rekognition hängen also stark zusammen, wenn man das “richtige” Modell anwendet.
Das Exemplarmodell lässt sich in drei Formeln ausdrücken:
\[ d_{ij} = \left(\sum_{k = 1}^K [x_{ik} - x_{jk}]^2\right)^{\frac{1}{2}} \]
\[ s_{ij} = e^{-c \times d_{ij}} \]
\[ P(R_i = A|i) = \frac{\sum_{j \in A} s_{ij}}{\sum_{j \in A} s_{ij}+\sum_{j \in B} s_{ij}} \]
Wir gehen das Modell nun schrittweise anhand eines Beispiels durch, damit wir verstehen, was die Formel bedeuten und welche Vorhersagen man mit dem Modell machen kann.
Distanz
Das Exemplarmodell nimmt an, dass wir, wenn wir einen neuen Stimulus wie z. B. ein Gesicht kategorisieren, das neue Gesicht mit allen Gesichtern vergleichen, die wir in der Vergangenheit gesehen haben und bei denen wir wissen, zu welcher Familie sie gehören.
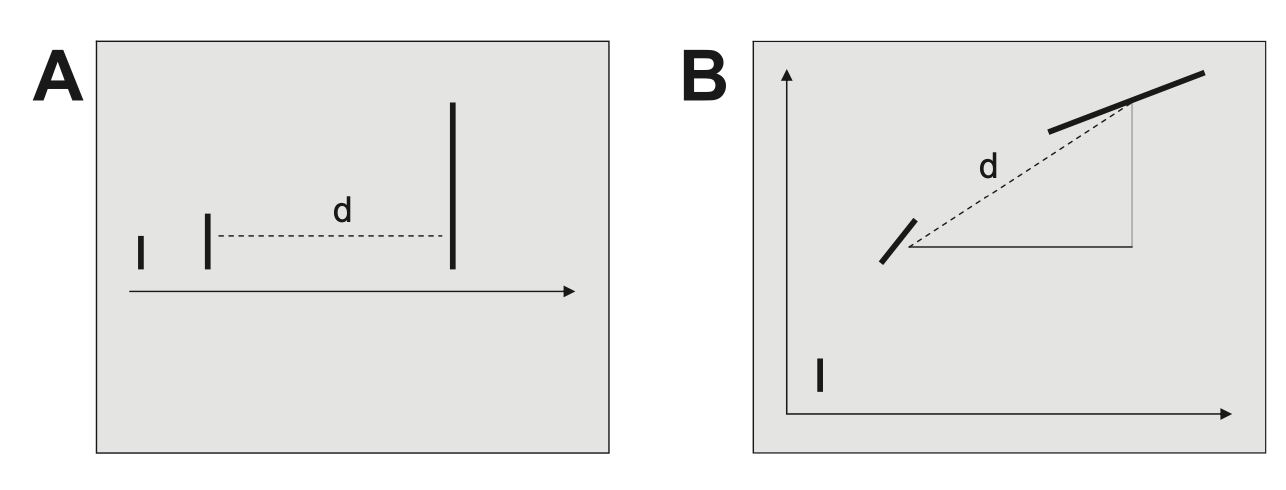
Ausprägungen auf Eigenschaften lassen sich in einem Koordinatensystem eintragen. In der Abbildung A sind Balken zu sehen, die unterschiedlich groß sind. Je größer, desto weiter rechts sind diese auf der Skala angeordnet. In Abbildung B kommt zu der Größe noch der Winkel als zweite Dimension auf der y-Achse hibzu. Je stärker der Balken gekippt ist, desto höher ist dieser auf der y-Achse eingezeichnet. Wenn wir eine weitere Dimension hinzunehmen (z.B. Stärke der Blaufärbung) hätten wir eine weitere Dimension und würden uns in einem dreidimensionalen Koordinatensystem befinden, usw. Die Eigenschaften von Stimuli lassen sich also skalieren.
Die Ähnlichkeit von Stimuli lässt sich nun als die euklidische Distanz zwischen den Stimuli im Koordinatensystem operationalisieren.
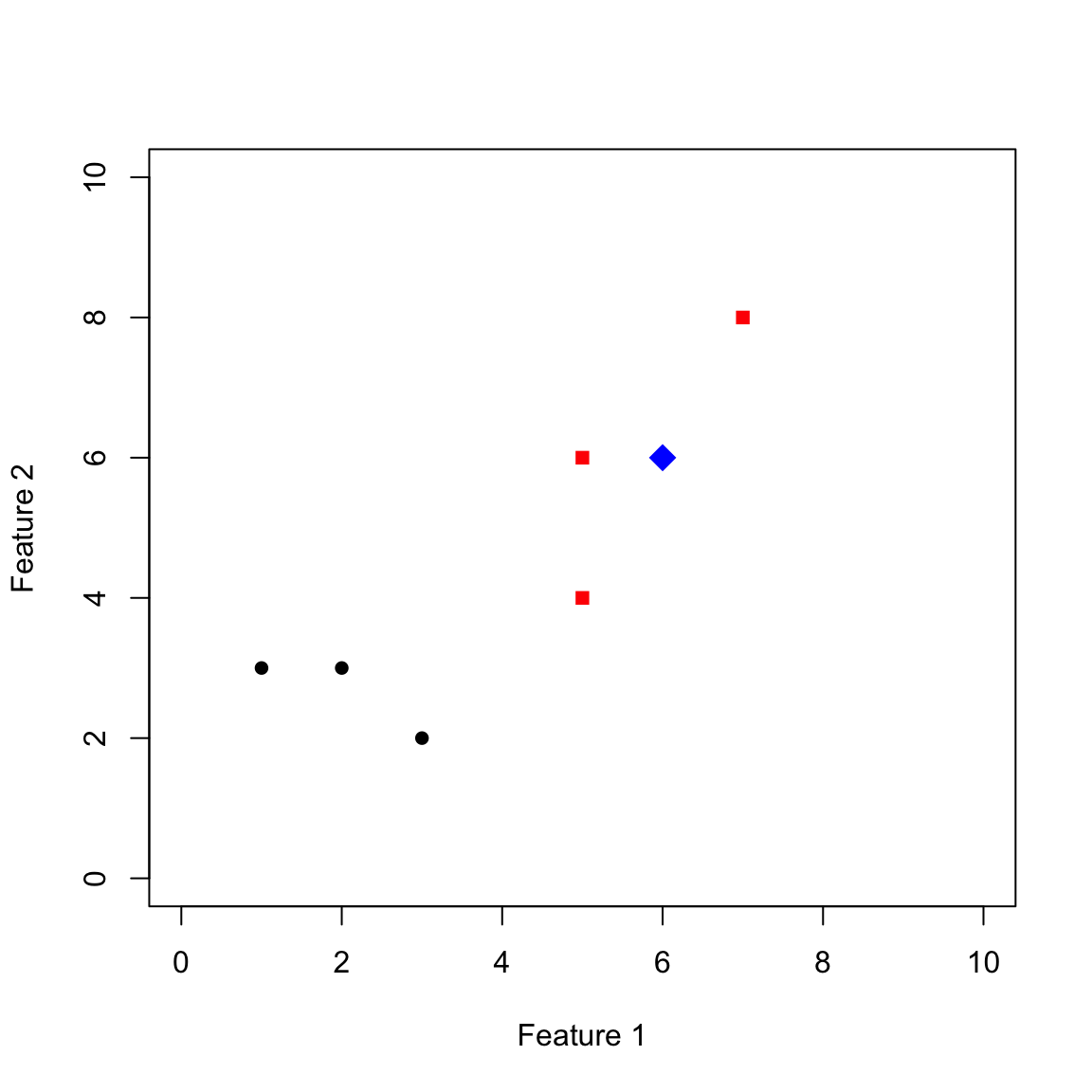
Schauen wir uns nun ein Beispiel an. In der Abbildung unten sind 7 Stimuli mit zwei Eigenschaften (= 2-dimensionales Koordinatensystem) eingezeichnet. Die schwarzen und roten Punkte wurden in der Lernphase präsentiert und ihre Kategorienzugehörigkeit benannt. Die schwarzen Punkte gehören zu einer Kategorie, die roten zu einer anderen Kategorie. In der Testphase wird nun der blaue Stimulus gezeigt. Welcher Kategorie wird dieser nun laut Modell zugeordnet.
Show code
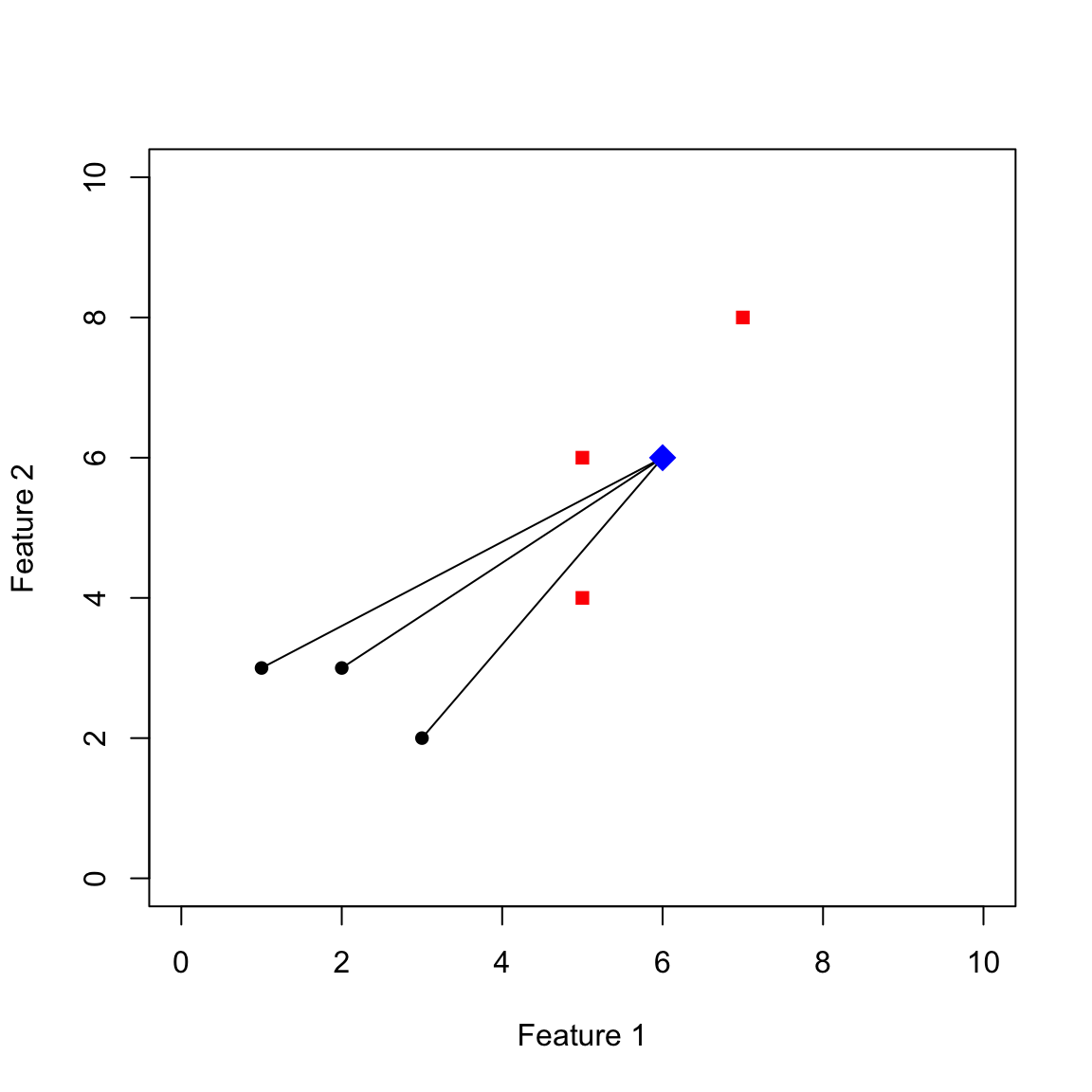
Im ersten Schritt berechnen wir alle Distanzen vom neuen Stimulus zu den Stimuli der schwarzen Kategorie. Diese sind in der folgenden Abbildung eingezeichnet:
Show code
A = rbind(
c(1,3),
c(3,2),
c(2,3)
)
B = rbind(
c(5,6),
c(7,8),
c(5,4)
)
plot(A,ylim = c(0,10),xlim=c(0,10),pch = 16,xlab="Feature 1",ylab = "Feature 2")
points(B,ylim = c(0,10),xlim=c(0,10),pch = 15,col="red")
new_point = c(6,6)
for(loop in 1:3){
lines(c(new_point[1],A[loop,1]),c(new_point[2],A[loop,2]))
}
points(new_point[1],new_point[2],pch=18,col="blue",cex=2)
Wie rechnen wir die Distanzen konkret aus? Der neue Stimulus hat folgende x und y-Koordinaten.
Show code
new_point
[1] 6 6Die Punkte der schwarzen Kategorie haben folgende Koordinaten.
Show code
A
[,1] [,2]
[1,] 1 3
[2,] 3 2
[3,] 2 3Die Distanz rechne ich nun nach Pythagoras nach folgender Formel: \(d_{ij} = \left(\sum_{k = 1}^K [x_{ik} - x_{jk}]^2\right)^{\frac{1}{2}}\). Konkret bedeutet das: Ich ziehe für jeden Vergleich die \(k = 2\) Koordinaten der beiden Stimuli voneinander ab, quadriere das Ganze, summiere es auf und ziehe daraus die Wurzel. Das passiert in den folgenden Schritten:
[1] 5.830952 5.000000 5.000000Nun Vergleiche ich den neuen Stimulus mit der roten Kategorie und rechne die Distanzen nach dem gleichen Prinzip aus.
Show code
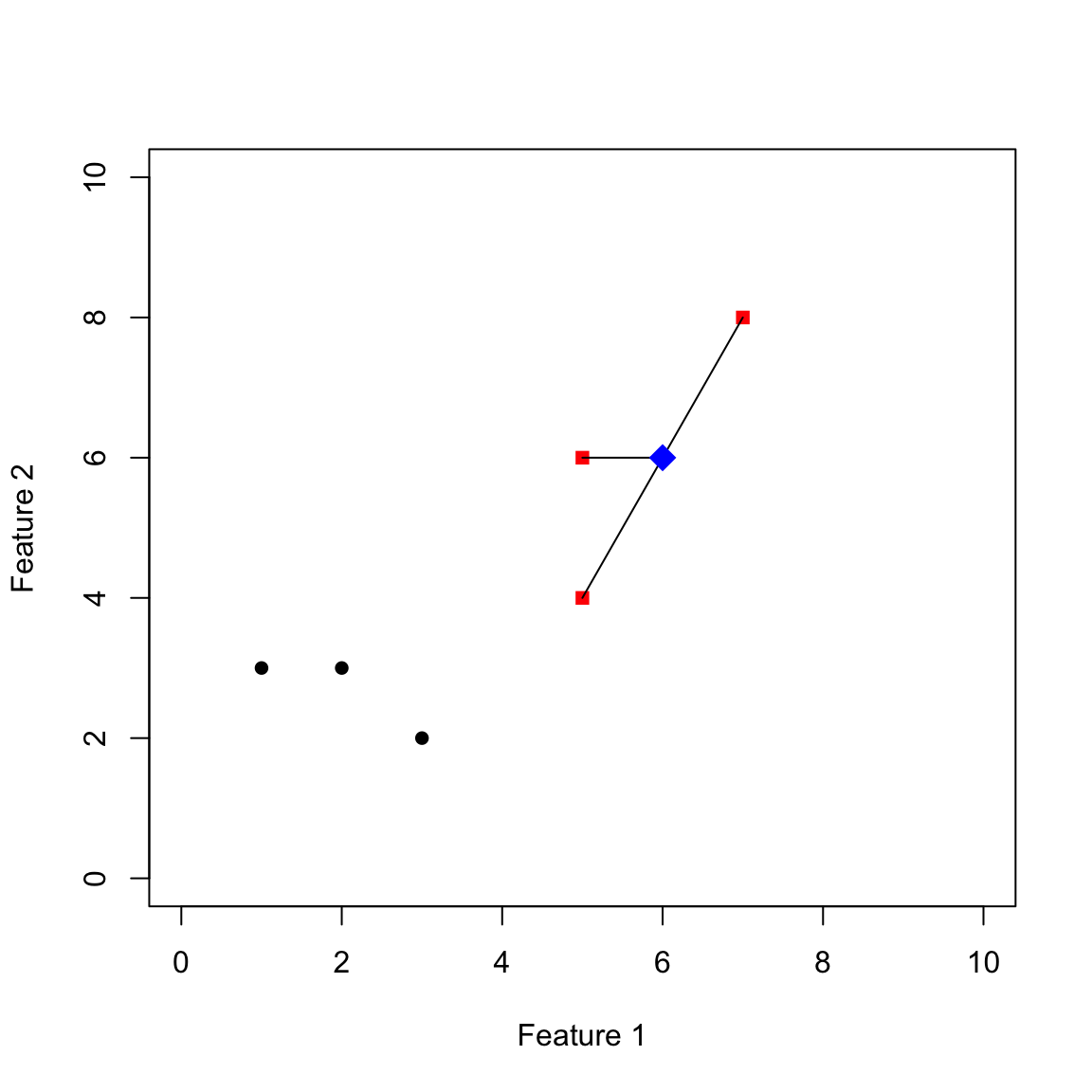
Die Distanzen betragen:
[1] 1.000000 2.236068 2.236068Aktivation
Damit haben wir die erste Formel des Modells gemeistert. Im nächsten Schritt übersetzen wir die Distanzen in Aktivationen nach der Formel \(s_{ij} = e^{-c \times d_{ij}}\). Bevor wir und die Details der Formel anschauen, plotten wir diese einmal (für ein \(c = .5\)).
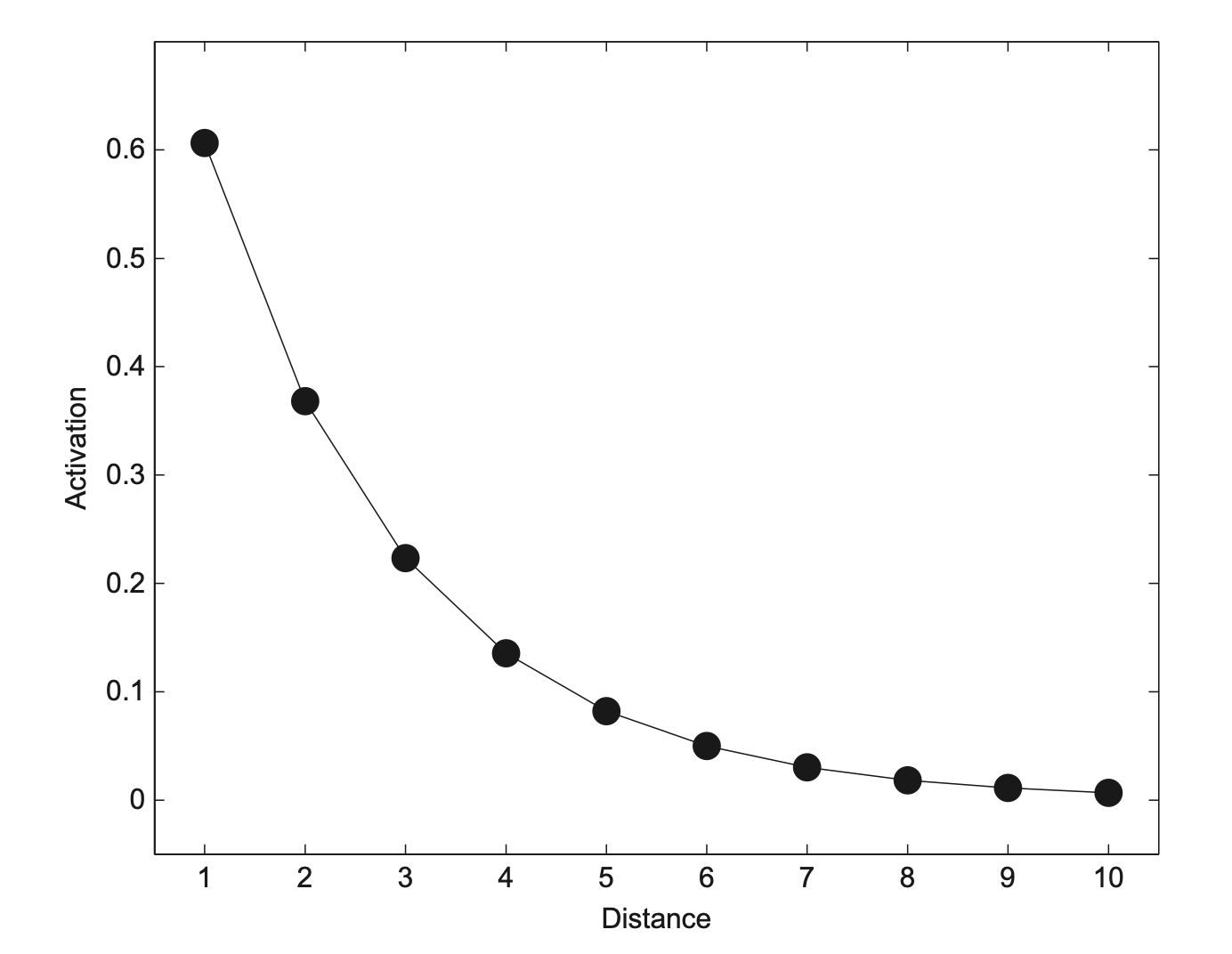
Auf der x-Achse befindet sich die Distanz zwischen zwei Stimuli, auf der y-Achse die zugehörige Aktivation. Je näher sich zwei Stimuli sind, d.h. je geringer die Distanz ist, desto mehr Aktivität erhält der Vergleich. Die Kurve fällt anfangs stark ab und läuft dann approximativ nach 0 aus, je weiter die Distanz zwischen zwei Stimuli ausfällt.
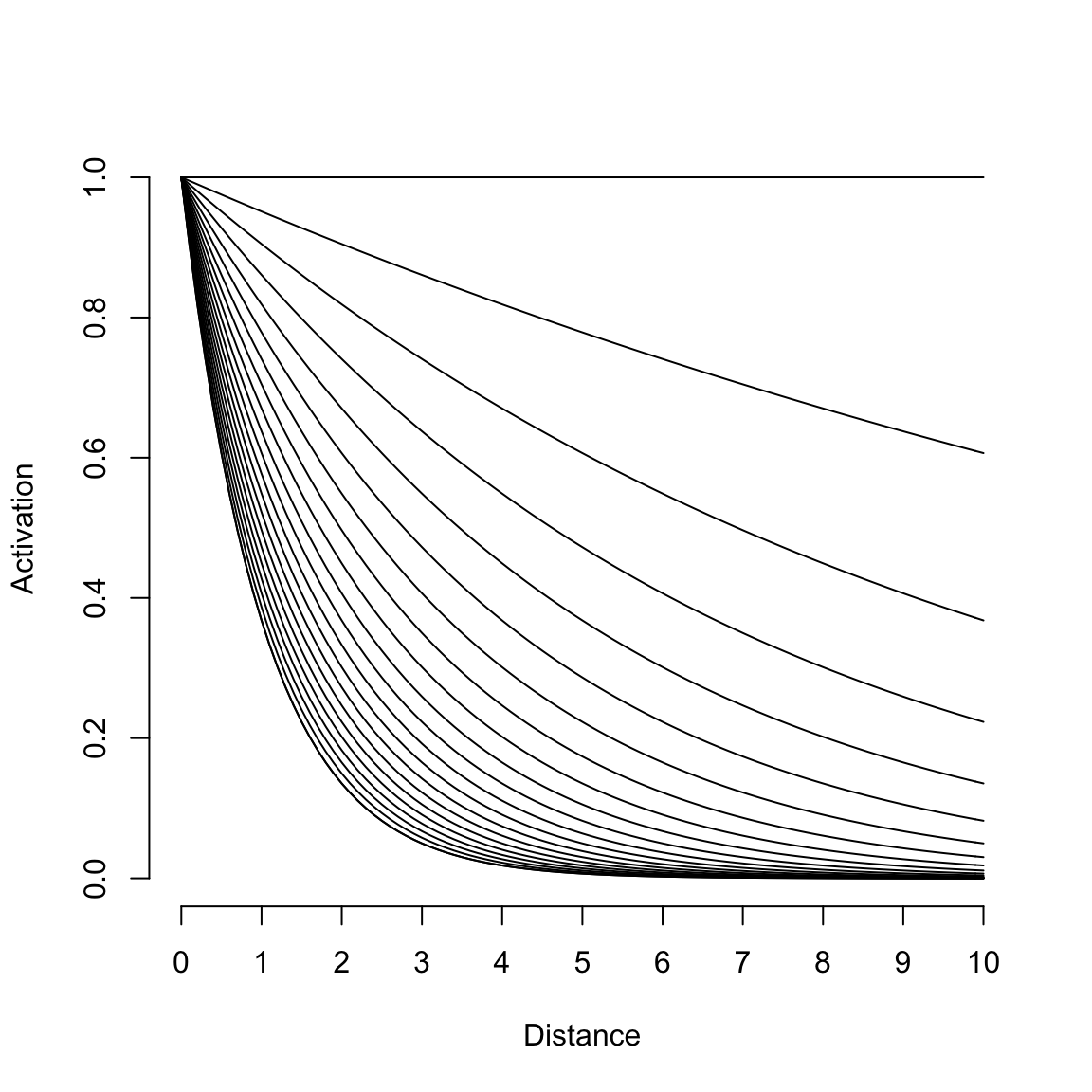
In der zugehörigen Formel \(s_{ij} = e^{-c \times d_{ij}}\) befindet sich \(c\). Je nachdem, welchen Wert dieses annimmt, verändert sich die Stärke des Abfalls. In der folgenden Abbildung ist die Kurve mit unterschiedlichen Werten für c eingezeichnet. Die flache Kurve hat ein c von 0, je stärker die Steigung, desto größer das c. Das heißt, je größer das c ausfällt, desto näher müssen sich die Stimuli sein, damit sie als ähnlich (= hohe Aktivation) wahrgenommen werden.
Show code
Für unser Beispiel ergeben sich folgende Aktivationen für die drei Stimuli der schwarzen Kategorie.
Show code
s_A = exp(-.5 * d_A)
s_A
[1] 0.05417824 0.08208500 0.08208500Die Aktivationen für die drei Stimuli der roten Kategorie ergeben:
Show code
s_B = exp(-.5 * d_B)
s_B
[1] 0.6065307 0.3269219 0.3269219Im vorletzten Schritt berechnen wir die Summe der Aktivationen pro Kategorie.
Für die schwarze Kategorie ergibt sich:
Show code
sum(s_A)
[1] 0.2183482Für die rote Kategorie ergibt sich:
Show code
sum(s_B)
[1] 1.260374Hier lässt sich schon erkennen, dass die Summe für die schwarze Kategorie niedriger asufällt. Der neue Stimulus ist also der roten Kategorie ähnlicher. Übersetzt in eine Kategorisierungswahrscheinlichkeit bedeutet das, dass die Wahrscheinlichkeit, den neuen Stimulus in die schwarze Kategorie einzuordnen unter .5 (= Zufall) liegt.
Wahrscheinlichkeit
Um die exakte Wahrscheinlichkeit zu berechnen, wenden wir die letzte Formel im Modell an: \(P(R_i = A|i) = \frac{\sum_{j \in A} s_{ij}}{\sum_{j \in A} s_{ij}+\sum_{j \in B} s_{ij}}\). Diese Formel sagt nur aus, dass wir die Summe der Aktivationen der schwarzen Kategorie in den Zähler setzen und durch die Summen aller Aktivationen teilen. Die Formel garantiert, da es keine negativen Aktivationen gibt (siehe vorherige Formel) und der Zähler niemals größer als der Nenner sein kann, dass wir Werte zwischen 0 und 1 erhalten. Das ist genau die Skalierung, die wir für Wahrscheinlichkeiten benötigen.
In der folgenden Abbildung ist die Funktion mit der beobachteten Summe der Aktivationen in der Kategorie B bei 1.26 und variabler Summe der Aktivationen der Kategorie A eingezeichnet. Die gestrichelte Linie deutet den beobachteten Summenwert der Kategorie A von .22 an und die zugehörige Wahrscheinlichkeit an.
Show code
s_A_example=seq(0,5,.1)
s_A = sum(s_A)
s_B = sum(s_B)
p = function(s_A_example,s_B){s_A_example/(s_A_example+s_B)}
plot(s_A_example,p(s_A_example,s_B),type="l", xlab = "s in A",ylab = "P(A)",axes=F,
ylim = c(0,1),main=paste("s in B =",round(s_B,2)))
axis(1,seq(0,5,.5),seq(0,5,.5))
axis(2,seq(0,1,.1),seq(0,1,.1))
pA = p(s_A,s_B)
abline(v=s_A,col="grey",lty=3)
abline(h=pA,col="grey",lty=3)
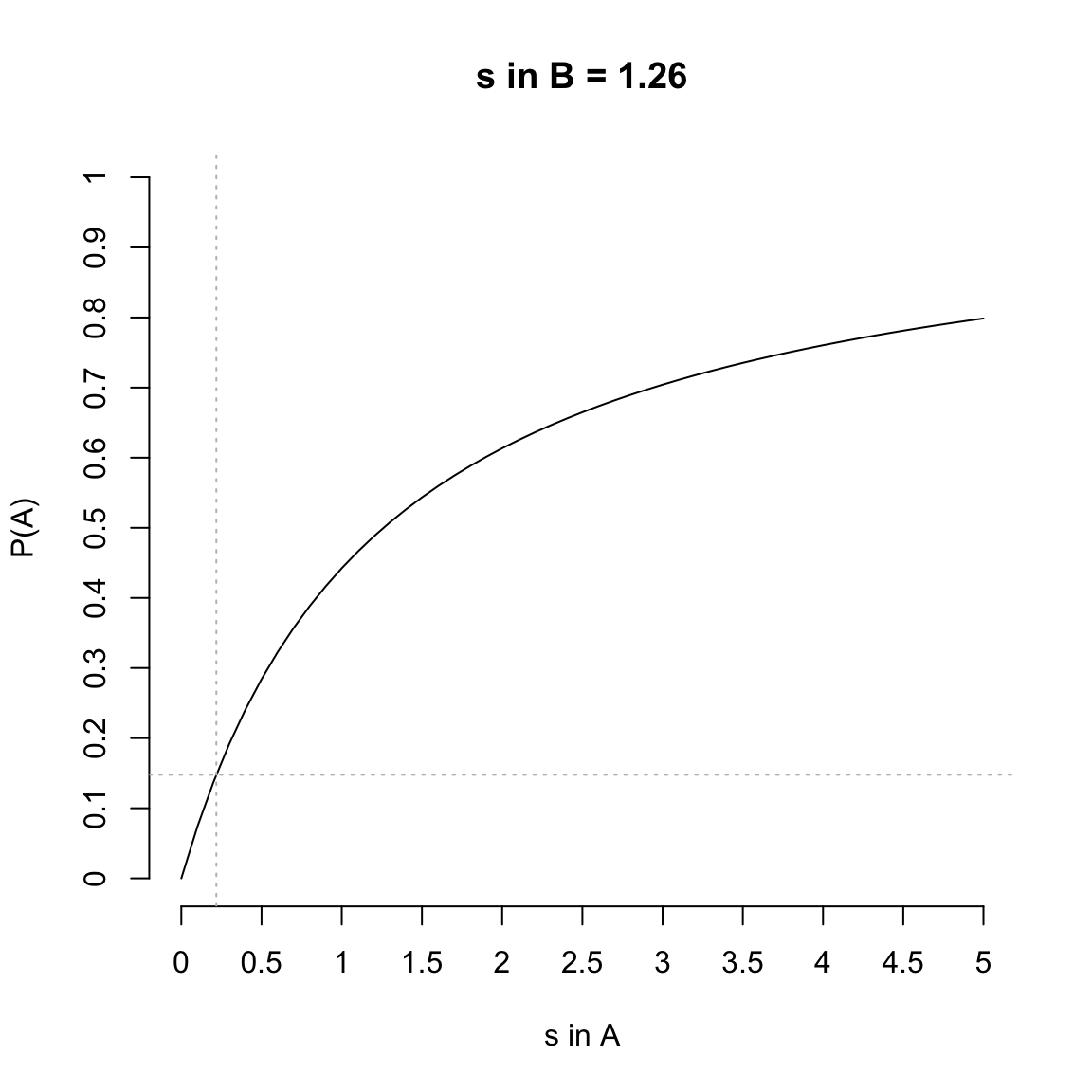
Die Wahrscheinlichkeit, den neuen Stimulus der Kategorie A zuzuordnen, liegt bei:
Show code
pA
[1] 0.14766Somit liegt die Wahrscheinlichkeit, den Stimulus der Kategorie B zuzuordnen, bei knapp 85%.
Zur Veranschaulichung sieht man in der folgenden Abbildung für alle möglichen neuen Stimuli im Bereich der ganzen Zahlen zwischen 0 bis 10 die Wahrscheinlichkeit für eine Kategorisierung in Kategorie A. Je heller das blau, desto größer die Wahrscheinlichkeit für eine A Kategorisierung. Die eingekringelten Stimuli markieren das Maximum (linke untere Ecke) oder Minimum (obere rechte Ecke) dieser Wahrscheinlichkeit.
Show code
A = rbind(
c(1,3),
c(3,2),
c(2,3)
)
B = rbind(
c(5,6),
c(7,8),
c(5,4)
)
new_point = expand.grid(0:10,0:10)
p_A_total = rep(NA,nrow(new_point))
for(loop in 1 : nrow(new_point)){
new_point_loop = unlist(new_point[loop,])
d_A = sqrt(rowSums(t(new_point_loop- t(A))^2))
d_B = sqrt(rowSums(t(new_point_loop- t(B))^2))
s_A = sum(exp(-.5 * d_A))
s_B = sum(exp(-.5 * d_B))
p_A = s_A / (s_A + s_B)
p_A_total[loop] = p_A
}
res = data.frame(new_point,p_A_total)
colnames(res) = c("x","y","p_A")
all_points = data.frame(rbind(cbind(A,1),cbind(B,2)))
colnames(all_points) = c("x","y","group")
all_points$group = factor(all_points$group)
levels(all_points$group) = c("A","B")
library(ggplot2)
index = c(which(res$p_A == max(res$p_A )),which(res$p_A == min(res$p_A )))
max_min_res = res[index,]
ggplot(res,aes(x=x,y=y,color = p_A)) +
geom_point(size=2.5,shape=15) +
geom_point(all_points,mapping=aes(x=x,y=y,shape=group),size=6) +
geom_point(max_min_res,mapping=aes(x=x,y=y),color="red",shape=1,size=6)+
scale_y_continuous(breaks = seq(0, 10, by = 1))+
scale_x_continuous(breaks = seq(0, 10, by = 1))
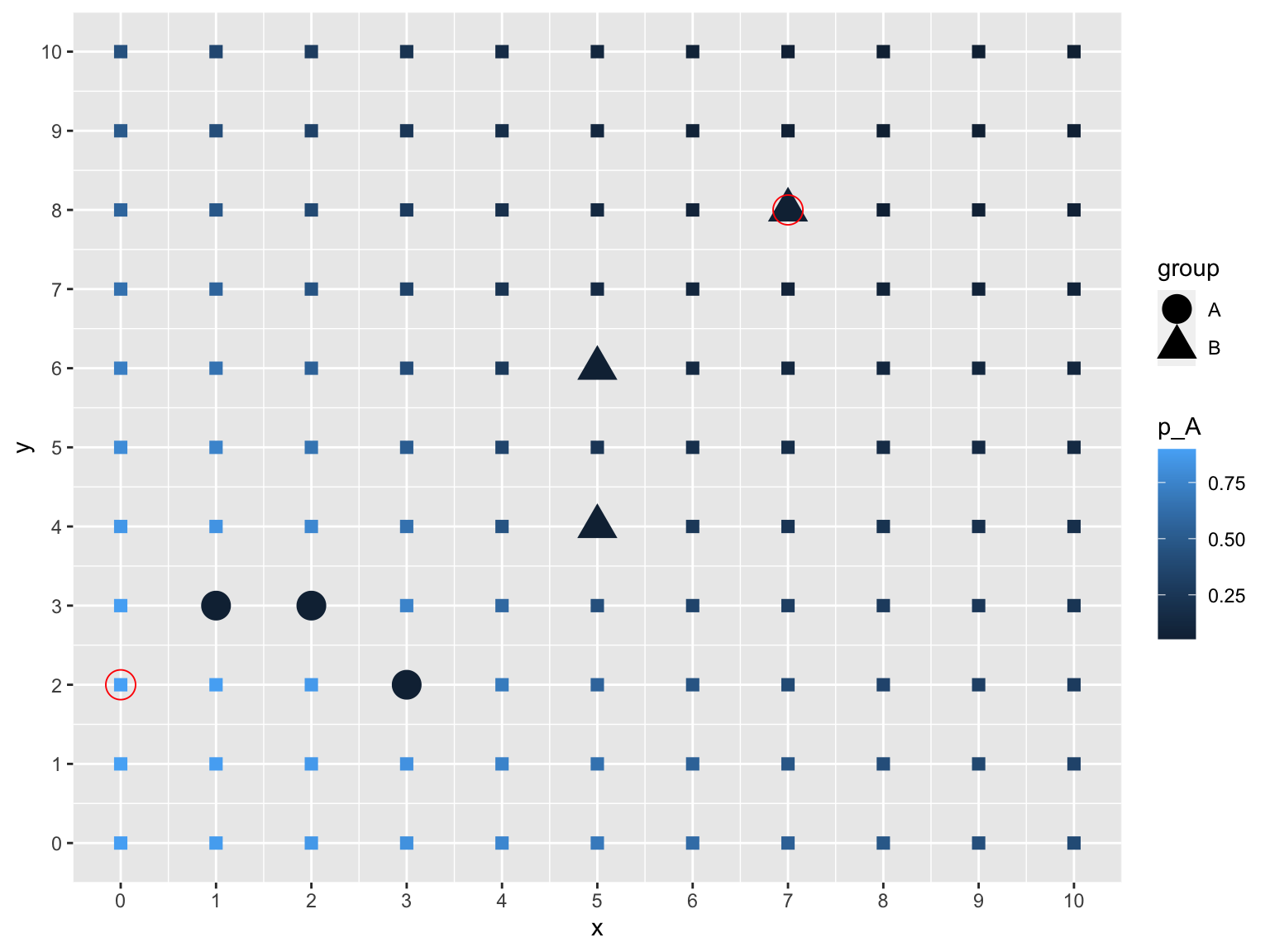
Interessanterweise sind es nicht die Stimuli, die mittig zu den Stimuli von Kategorie A oder B liegen, die zu maximalen oder minimalen Wahrscheinlichkeiten führen. Das ist beim ersten Nachdenken möglicherweise gegenintuitiv und ein verbales Modell hätte uns wahrscheinlich auf die falsche Fährte geführt. Der Grund dafür ist, dass Stimuli für eine möglichst eindeutige Kategorisierung (= hohe oder niedrige Wahrscheinlichkeit) maximal nah an den Stimuli der einen Kategorie und maximal weit weg von den Stimuli der anderen Kategorie liegen sollten.
A-priori Kriterium: Falsifizierbarkeit
Wenn wir Daten aus dem Labor vorliegen haben, können wir testen, wie gut unser Modell die Daten beschreiben kann (= post-hoc Kriterium). Wir können jedoch auch bevor wir in das Labor gehen (= a-priori Kriterium) die Güte eines Modells über den empirischen Gehalt nach Popper (1935) bewerten.
Der empirische Gehalt setzt sich aus der Allgemeinheit und der Präzision eines Modells zusammen. Wir möchten Modelle haben, die möglichst allgemein sind (d.h., sich auf viele Situationen, Probandegruppen, etc., anwenden lassen) und dabei möglichst präzise Vorhersagen machen (d.h., viele mögliche Beobachtungen verbietet).
Hypothesen werden ja als “wenn…dann…” Sätze formuliert wie z. B. “Wenn eine Person frustriert wird, reagiert sie aggressiv.” Die Allgemeinheit bezieht sich auf den “wenn”-Teil im Satz: Im Beispiel gilt die Hypothese für alle Personen, d.h., Kinder, Erwachsene, etc., sie ist also relativ allgemein. Die Präzision bezieht sich auf den “dann”-Teil im Satz: Die Hypothese ist nicht sehr präzise, es wird nur vorhergesagt, dass aggressives Verhalten beobachtbar sein sollte, wie stark dieses ist oder wie es mit dem Grad der Frustration zusammenhängt, ist nicht spezifiziert.
Wie sieht eine präzisere Vorhersage für die Frustrations-Aggressions-Hypothese aus?
Ein Modell ist dann falsifizierbar, wenn es bestimmte Beobachtungen verbietet: In unserem Beispiel wäre freundliche Verhalten nach einer Frustration nicht hypothesenkonform. Ein hoher Grad an Falsifizierbarkeit ist ein erstrebenswertes Merkmal: Diese Modelle machen spezifischere und damit nützlichere Vorhersagen und diese Modelle sind einfacher zu widerlegen.
Roberts & Pashler (2000) haben die Idee der Präzision in folgender Abbildung zusammengefasst.
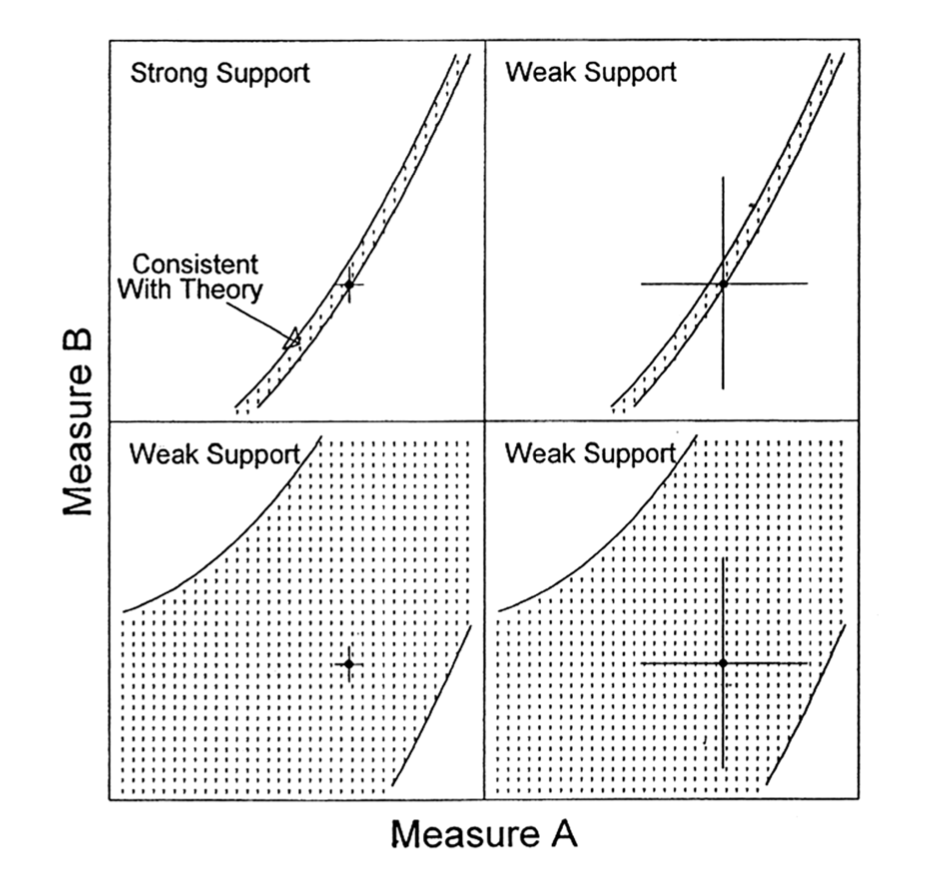
Jede Zelle in der Vierfeldertafel beschreibt die Vorhersagen eines Modells (Punkte) und die empirische Beobachtung (Kreuz mit Messfehlerbalken) bei zwei hypothetischen Maßen (= Achsen) wie z. B. Rekognitionswahrscheinlichkeit und Kategorisierungswahrscheinlichkeit.
Das Modell in der ersten Zeile ist sehr viel präziser, nur wenige potentielle Beobachtungen sind hypothesenkonform. Das Modell in der zweiten Zeile ist weniger präzise, man sieht viel weniger weiße Flächen, die mögliche hypotheseninkonforme Beobachtungen darstellen.
Obwohl der Datenpunkt für beide Modelle hypothesenkonform ist, ist das Modell in der ersten Zeile nach dem a-priori Kriterium der Präzision besser aufgestellt. Wie sieht es mit der Allgemeinheit der Modelle aus? Beide Modelle machen Aussagen über die beiden Maße, sie sind also in diesem Beispiel ähnlich allgemein.
In Glöckner & Betsch (2011) und Jekel (2019) finden Sie eine Diskussion aktueller Modelle aus der Entscheidungspsychologie unter einem Popperianischen Blickwinkel. Für eine sehr lesenswerte Einführung in die Wissenschaftstheorie unter einem psychologischen Blickwinkel ist das Buch von Dienes (2008) empfehlenswert. Sie finden Auszüge aus dem Buch hier.
Leitfragen für die Diskussion
Was passiert im Modell, wenn wir unterschiedlich viele Stimui pro Kategorie haben?
Wie lassen sich Reihenfolgeeffekte in der Lernphase im Modell abbilden?
Lässt sich das Modell auch auf die Kategorisierung in sozialen Gruppen anwenden?
Welche Einflüsse haben dabei ggf. Stereotypen und wie lassen sich diese im Modell aufnehmen?
Kategorisierungsdimensionen können mehr oder weniger salient sein. Wie lässt sich Salienz im Modell integrieren und wie könnte man testen, ob das erweiterte Modell Salienzeffekte beschreiben kann?
Ist das vorgestellte Kategorisierungmodell ein gutes oder schlechtes Modell? Wie lässt sich die Güte des Modells bestimmen? Welche a-priori und welche post-hoc Kriterien lassen sich für eine Bewertung heranziehen?